Solving Contextual Bandits with Greediness
In this post, I will explain and implement Epsilon-Greedy, a simple algorithm that solves the contextual bandits problem. Despite its simplicity, this algorithm performs considerably well [1].
Prerequisites
- A Very Short Intro to Contextual Bandits
- Python
- Numpy
- (Optional) Standard Multi-Armed Bandit Epsilon-Greedy Algorithm [2]
- Logistic Regression (You need to know what it is, not necessarily how it works)
* Note: In this article, I use the words arm and action, and the words step and round, interchangeably.
Intro
The intuition of the algorithm is to choose random actions at sometimes. In the rest of the time, it chooses the action that it thinks is the best one. This simple balance between exploration (random actions) and exploitation (greediness) yields good results.
Pseudocode

This pseudocode is from [3].
Input
We can see that the algorithm receives three arguments, a probability p, a decay rate d and the oracles $\hat{f}_{1: k}$. Let’s explain each one of them.
- p: Dictates what will be the probability of a random action in each round.
- d: This variable controls how fast p decreases during training.
- $\hat{f}_{1: k}$: Oracles that are classifiers or regressors. They learn the rewards that each action will return, given the context x.
Line-by-Line Analysis
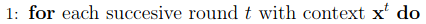
This is the standard loop of contextual bandits, in which the algorithm receives a context x in each round.
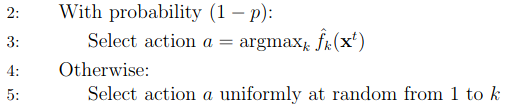
In this block, the algorithm chooses a random action with probability p. Otherwise, it chooses the action that gives the maximum reward according to the oracles.
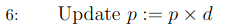
The probability rate is decreased according to d.
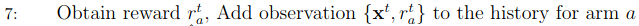
The algorithm receives a reward $r_a^t$ and stores it together with the observed context $x^t$. Note that the data stored is exclusive to the performed action/arm a.
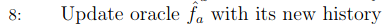
Then, the oracles learn the reward of each (context, action) pair given the data history. This training does not need to happen in every round. It is possible, for example, to train the oracles every 50 rounds.
Code
The programming language used in this implementation is Python and the full implementation is available here. For simplicity, the decay rate d will be discarded and it will be assumed that the probability of a random action will remain constant. Only binary rewards will be used. For the oracles, logistic regressors of the Sklearn library have been chosen.
Contextual Environment
I made an interface of the contextual bandits environment so that I can easily request contexts and get rewards by acting on the environment.
class ContextualEnv(ABC):
@abstractmethod
def get_context(self) -> np.ndarray:
pass
@abstractmethod
def act(self, action: int) -> float:
pass
@abstractmethod
def get_num_arms(self) -> int:
pass
@abstractmethod
def get_context_dim(self) -> int:
pass
Epsilon Greedy Constructor
class EpsilonGreedy:
def __init__(self, c_env: ContextualEnv,
epsilon: float, num_steps: int,
training_freq: int):
self.num_arms = c_env.get_num_arms()
self.num_steps = num_steps
self.epsilon = epsilon
self.training_freq = training_freq
self.classifiers = [LogisticRegression() for _ in
range(self.num_arms)]
context_dim = c_env.get_context_dim()
self.context_data = np.zeros((num_steps,
context_dim))
self.rewards_data = np.full((num_steps,
self.num_arms), -1,
dtype=float)
self.c_env = c_env
Here, epsilon is the probability of a random action p of the pseudocode. This class also receives a contextual environment object, the number of steps/rounds, and a parameter that dictates the training frequency of the oracles.
One logistic regressor oracle is initialized for each arm/action of the environment. The context and reward history are also initialized. Since binary rewards are being used, the reward history is filled with -1, so it is possible to differentiate what arm received a reward in each round (a value of -1 says that the respective arm was not used in a given round).
Save Step/Round
def save_step(self, context: np.ndarray, action: int,
reward: float, step: int) -> None:
self.context_data[step] = context
self.rewards_data[step, action] = reward
This method saves the context and reward received in each round/step. Note that the reward is saved on the history of the action/arm used.
Action Policy
def action_policy(self, context: np.ndarray) -> int:
coin = random.uniform(0, 1)
if coin > self.epsilon:
action = self.greedy_action(context)
else:
action = random.randint(0, self.num_arms-1)
return action
This method determines which strategy will be chosen, exploration or exploitation. The random action is chosen with a probability equal to epsilon, the greedy action is chosen otherwise.
Greedy Action
def greedy_action(self, context: np.ndarray) -> int:
rewards = np.zeros(len(self.classifiers))
for index, classifier in enumerate(self.classifiers):
try:
context = context.reshape(1, -1)
action_score = classifier.predict(context)
except NotFittedError as e:
a = 3.0/self.num_arms
action_score = np.random.beta(a, 4)
rewards[index] = action_score
max_rewards = max(rewards)
best_actions = np.argwhere(rewards == max_rewards)
best_actions = best_actions.flatten()
return np.random.choice(best_actions)
On the greedy action method, each classifier is evaluated based on the context. If the classifier has not yet been trained, the score is estimated by running a beta distribution. This trick is done on [3]. Afterwards, the action with the maximum estimated reward is chosen.
Fit
def fit(self, step: int) -> None:
step += 1
contexts_so_far = self.context_data[:step]
rewards_so_far = self.rewards_data[:step]
for arm_index in range(self.num_arms):
self.fit_classifier(contexts_so_far,
rewards_so_far, arm_index)
In this method, each classifier is trained, only the contexts and rewards seen so far are used.
def fit_classifier(self, contexts: np.ndarray,
rewards: np.ndarray,
arm: int) -> None:
arm_rewards = rewards[:, arm]
# get the index of the rewards that the arm saw
index = np.argwhere(arm_rewards != -1)
index = index.flatten()
arm_rewards = arm_rewards[index]
# test if the arm saw at least one example of
# each class
if len(np.unique(arm_rewards)) == 2:
arm_contexts = contexts[index]
self.classifiers[arm].fit(arm_contexts,
arm_rewards)
Here, only the rewards that the each arm saw are used (that is why the
reward history was initialized with -1, note the argwhere). It is verified if the arm saw at least one example
of each reward (values of 0 and 1), so it can be trained.
Simulation
def simulate(self) -> np.ndarray:
"""Returns rewards per step"""
rewards_history = np.zeros(self.num_steps)
for step in range(self.num_steps):
context = self.c_env.get_context()
action = self.action_policy(context)
reward = self.c_env.act(action)
rewards_history[step] = reward
self.save_step(context, action, reward, step)
if step % self.training_freq == 0:
self.fit(step)
return rewards_history
The simulate method does the training itself. A context is observed, an action
is estimated based on the context, the (context, reward) is stored on the
respective arm history, and every training_freq steps, the oracles are trained.
Evaluation
Let’s evaluate the algorithm on three environments, taken from here. I will give a brief description of each one:
- Binary context and deterministic rewards (easiest).
- Binary context and stochastic rewards.
- Continuous context and stochastic rewards.
The results were obtained using epsilon equal to 0.2, training the oracles every 50 rounds and averaging the results of 100 runs. This plot considers the mean reward of all history until each round.
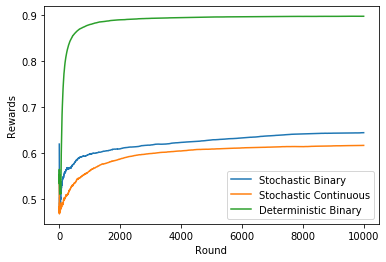
We can see that the algorithm learns the deterministic binary environment really fast. The performance on the stochastic binary and stochastic continuous environments are about the same, but the algorithm has a little more trouble to learn the continuous environment.
References
- [1] Bietti, Alberto, et al. “A Contextual Bandit Bake-Off.” ArXiv:1802.04064 [Cs, Stat], Jan. 2020. arXiv.org, http://arxiv.org/abs/1802.04064.
- [2] Chapter 2 of Richard S. Sutton and Andrew G. Barto. 2018. Reinforcement Learning: An Introduction. A Bradford Book, Cambridge, MA, USA. http://incompleteideas.net/book/the-book.html
- [3] Cortes, David. “Adapting Multi-Armed Bandits Policies to Contextual Bandits Scenarios.” ArXiv:1811.04383 [Cs, Stat], Nov. 2019. arXiv.org, http://arxiv.org/abs/1811.04383.